文章目录
[+]
牛顿法，作为一种经典的数值计算方法，广泛应用于数学、物理、工程等领域。本文将从牛顿法的原理出发，结合实际程序代码，深入剖析牛顿法的实现过程，旨在为广大读者提供一种高效、实用的数值计算方法。
一、牛顿法原理
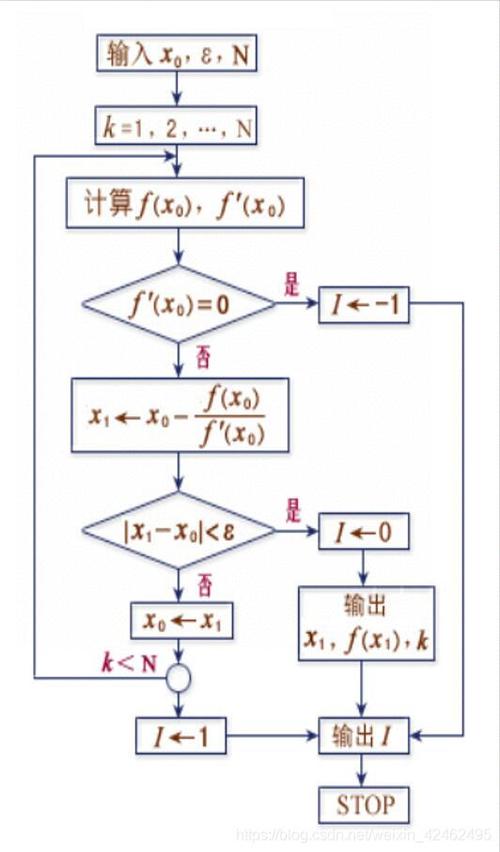
牛顿法，又称为牛顿-拉弗森迭代法，是一种求解非线性方程根的方法。其基本思想是将非线性方程转化为线性方程，通过迭代逼近方程的根。设f(x)为待求根的非线性方程，则牛顿法的迭代公式为：
（图片来自网络侵删）
x_{n+1} = x_n - \\frac{f(x_n)}{f'(x_n)}
其中，x_{n+1}为第n+1次迭代的近似根，x_n为第n次迭代的近似根，f(x)为非线性方程，f'(x)为f(x)的导数。
二、牛顿法程序代码实现
以下是一个基于Python的牛顿法程序代码示例：
```python
def newton_method(f, df, x0, tol=1e-10, max_iter=100):
\
