在数学、计算机科学、人工智能等领域,问题求解是一个永恒的主题。面对复杂的问题,如何找到最优解或近似解,成为研究人员关注的焦点。其中,回溯法作为一种经典的算法设计方法,以其独特的优势在众多问题求解领域中发挥着重要作用。本文将从回溯法的原理、应用、优势等方面进行探讨,以期为广大读者揭示这一智慧之匙的奥秘。
一、回溯法原理

回溯法,又称试探法,是一种通过递归尝试所有可能的解,并从中筛选出满足条件的解的算法。其基本思想是从问题的部分解出发,按照一定规则向前试探,若试探过程中发现当前解不满足条件,则回溯到上一个状态,改变某个参数的值,再继续试探。如此反复,直至找到满足条件的解或所有可能的解。
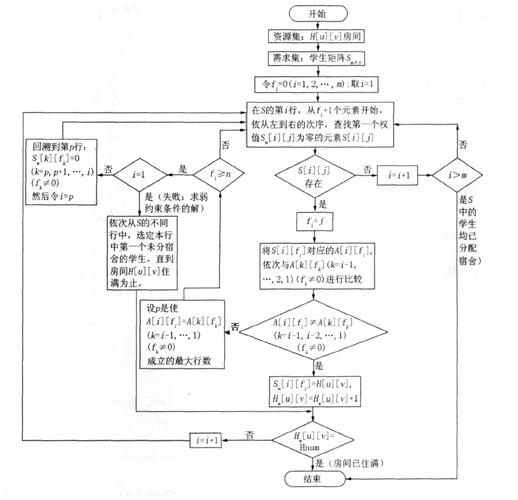
回溯法具有以下特点:
1. 递归实现:回溯法通常采用递归方式实现,通过递归调用自身,逐步探索问题的解空间。
2. 回溯机制:在试探过程中,若发现当前解不满足条件,则回溯到上一个状态,重新开始试探。
3. 状态空间搜索:回溯法通过搜索问题的解空间,逐步缩小搜索范围,直至找到满足条件的解。
二、回溯法应用
回溯法广泛应用于各个领域,以下列举几个典型应用:
1. 排列组合问题:如全排列、组合问题等。例如,求解n个不同元素的排列组合问题,可以使用回溯法进行求解。
2. 图着色问题:如图着色问题、哈密顿回路问题等。回溯法可以帮助我们找到满足条件的图着色方案或哈密顿回路。
3. 棋类游戏:如围棋、象棋等。回溯法可以帮助计算机进行棋局搜索,找到最佳走法。
4. 搜索问题:如迷宫搜索、路径规划等。回溯法可以帮助我们找到从起点到终点的最优路径。
三、回溯法优势
与其它算法相比,回溯法具有以下优势:
1. 通用性强:回溯法适用于各种问题求解场景,具有广泛的适用范围。
2. 简单易懂:回溯法的实现过程相对简单,易于理解和掌握。
3. 效率高:在许多问题求解场景中,回溯法具有较高的求解效率。
回溯法也存在一定的局限性。当问题规模较大时,回溯法的效率会显著降低,甚至陷入“组合爆炸”的困境。因此,在实际应用中,需要根据具体问题选择合适的算法或对其进行优化。
回溯法作为一种经典的算法设计方法,在众多问题求解领域中发挥着重要作用。通过对回溯法的深入研究,我们可以更好地把握问题的解空间,提高算法的求解效率。在未来的研究中,相信回溯法将会在更多领域得到应用,为人类智慧的发展贡献力量。






