在信息时代,数据已成为国家和社会发展的重要资源。如何从海量数据中提取有价值的信息,是当前数据科学领域的重要课题。样本熵作为一种有效的数据分析工具,在信息压缩、模式识别、故障诊断等方面具有广泛的应用前景。本文将对样本熵的概念、原理、算法以及在实际数据分析中的应用进行探讨。
一、样本熵的概念与原理

1. 概念
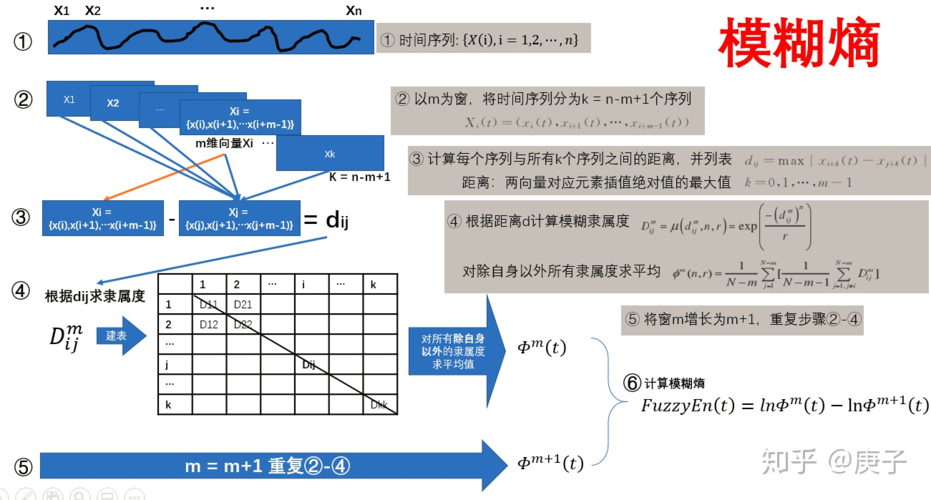
样本熵(Sample Entropy,SE)是由日本学者Shannon提出的熵概念在样本数据上的扩展。样本熵反映了一组样本序列的复杂程度,即系统的不确定性程度。样本熵越大,表示样本序列越复杂,不确定性越高。
2. 原理
样本熵的计算过程如下:
(1)将原始数据序列进行去噪处理,得到干净的数据序列。
(2)将数据序列分为m个长度为N的子序列。
(3)计算相邻子序列之间的距离,距离定义为两个子序列在对应位置上不同元素的个数。
(4)计算距离为d的相邻子序列对的比例,记为C(d)。
(5)计算样本熵S(m, d):
S(m, d) = -k∑_{i=1}^{k} P(i)logP(i)
其中,k为距离为d的相邻子序列对中,长度为m的子序列的个数;P(i)为第i个长度为m的子序列出现的概率。
二、样本熵的算法
样本熵的计算过程涉及多个步骤,主要包括以下算法:
1. 数据去噪
数据去噪是样本熵计算的前提,常用的去噪方法有滑动平均、中值滤波、高斯滤波等。
2. 子序列划分
根据设定的长度m,将数据序列划分为长度为m的子序列。
3. 距离计算
计算相邻子序列之间的距离,距离计算方法有多种,如欧氏距离、曼哈顿距离等。
4. 相邻子序列对比例计算
计算距离为d的相邻子序列对的比例。
5. 样本熵计算
根据公式计算样本熵。
三、样本熵在数据分析中的应用
1. 信息压缩
样本熵可以用来评估信息压缩的效果,通过比较压缩前后样本熵的变化,判断压缩方法的有效性。
2. 模式识别
样本熵可以用来识别不同类别数据之间的差异,如人脸识别、语音识别等。
3. 故障诊断
样本熵可以用来分析设备运行状态,通过监测样本熵的变化,发现设备故障。
4. 生物医学
样本熵可以用来分析生物医学数据,如心电图、脑电图等,有助于疾病的诊断。
样本熵作为一种有效的数据分析工具,在信息压缩、模式识别、故障诊断等方面具有广泛的应用前景。本文对样本熵的概念、原理、算法以及在实际数据分析中的应用进行了探讨,旨在为相关领域的研究者提供参考。随着数据科学技术的不断发展,样本熵将在更多领域发挥重要作用。






