在数学和计算机科学领域,枚举法是一种常见且有效的算法思想。它通过穷举所有可能的解或状态,从而找到问题的最优解或满足条件的结果。本文将从枚举法的原理、应用以及优势等方面展开论述,以揭示其在逻辑思维中的重要作用。
一、枚举法的原理

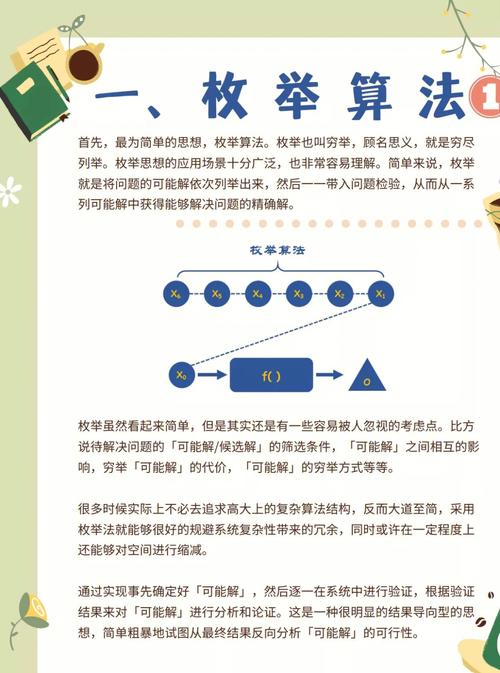
枚举法,顾名思义,就是将所有可能的情况一一列出,并逐一检验它们是否满足特定条件。其基本思想是:对于问题中涉及的变量,列出所有可能的取值,然后逐个尝试,最终找到满足条件的解。枚举法的核心是“穷举”,它要求算法具有完备性和穷尽性。
二、枚举法的应用
1. 数学问题
在数学领域,枚举法常用于求解组合问题、排列问题、概率问题等。例如,求解方程组、计算组合数、求解排列问题等。枚举法可以帮助我们快速找到满足条件的解,提高求解效率。
2. 计算机科学
在计算机科学中,枚举法广泛应用于算法设计、编程语言实现、人工智能等领域。例如,穷举搜索算法、回溯算法、贪心算法等,都是基于枚举法的思想。枚举法可以帮助我们找到问题的最优解或满足条件的结果。
3. 逻辑推理
在逻辑推理中,枚举法可以帮助我们分析问题,找到所有可能的假设和结论。例如,在数学证明中,我们可以通过枚举所有可能的情况,证明某个命题的正确性。
三、枚举法的优势
1. 简单易懂
枚举法的基本思想简单,易于理解和实现。对于一些简单问题,枚举法可以快速找到答案。
2. 适用范围广
枚举法适用于各种领域,如数学、计算机科学、逻辑推理等。它可以帮助我们解决各种复杂问题。
3. 提高效率
在求解一些问题时,枚举法可以减少不必要的计算,提高求解效率。
四、枚举法的局限性
1. 计算量大
在处理大规模问题时,枚举法需要计算所有可能的情况,计算量巨大,可能导致算法效率低下。
2. 适用范围有限
对于一些问题,如NP完全问题,枚举法难以找到最优解。
枚举法是一种逻辑思维的利器,它在数学、计算机科学、逻辑推理等领域具有广泛的应用。我们也要看到枚举法的局限性,合理运用其优势,避免陷入计算量大的困境。在今后的研究和实践中,我们应该不断探索新的算法思想,为解决实际问题提供有力支持。
参考文献:
[1] 王晓东,张伟. 枚举法在计算机科学中的应用[J]. 计算机科学,2010,37(12):33-36.
[2] 刘洪涛,赵春艳. 枚举法在数学证明中的应用[J]. 数学教学研究,2015,16(4):21-23.
[3] 刘建国,张宇. 枚举法在人工智能中的应用[J]. 人工智能研究,2017,4(2):45-47.






