一、贝塞尔曲线的起源与发展
贝塞尔曲线(Bezier Curve)是一种广泛应用于计算机图形学、工业设计、动画制作等领域的数学曲线。它最早由法国数学家皮埃尔·贝塞尔(Pierre Bézier)在20世纪50年代提出,因其简洁、优美的特性,被誉为“曲线之王”。

贝塞尔曲线的发展历程可以追溯到古希腊时期,当时的数学家们已经开始研究曲线的几何性质。直到20世纪,随着计算机技术的飞速发展,贝塞尔曲线才逐渐走进人们的视野。如今,贝塞尔曲线已成为计算机图形学中不可或缺的工具。
二、贝塞尔曲线的数学原理
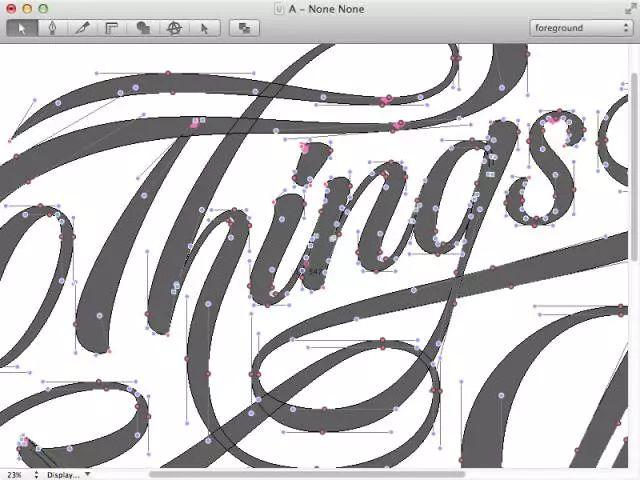
贝塞尔曲线的数学原理基于多项式函数。一条贝塞尔曲线由多个控制点(control points)和阶数(degree)决定。阶数表示曲线的复杂程度,阶数越高,曲线越复杂。
贝塞尔曲线的数学表达式为:
B(t) = Σ(Ci Bi,n t^n)
其中,B(t)为曲线上的点,Ci为控制点,Bi,n为贝塞尔基函数,t为参数。
三、贝塞尔曲线的应用领域
贝塞尔曲线在众多领域都有着广泛的应用,以下列举几个典型实例:
1. 计算机图形学:贝塞尔曲线在计算机图形学中应用广泛,如绘制直线、曲线、圆弧、椭圆等。贝塞尔曲线还用于三维建模、动画制作、图像处理等领域。
2. 工业设计:贝塞尔曲线在工业设计中具有重要作用,如汽车、飞机、船舶等产品的造型设计。设计师可以利用贝塞尔曲线轻松地创造出流畅、优美的曲线形状。
3. 动画制作:动画制作中,贝塞尔曲线常用于描述物体运动的轨迹。通过调整控制点,动画师可以精确控制物体的运动状态,实现平滑、自然的动画效果。
4. 地理信息系统(GIS):贝塞尔曲线在GIS中用于地图绘制、路径规划等方面。通过贝塞尔曲线,可以绘制出更加精确、美观的地图。
四、贝塞尔曲线的优势与局限性
贝塞尔曲线具有以下优势:
1. 简洁性:贝塞尔曲线的数学表达式简洁,便于计算和编程。
2. 可控性:通过调整控制点,可以轻松地改变曲线的形状和大小。
3. 美观性:贝塞尔曲线具有优美的几何性质,适用于各种造型设计。
贝塞尔曲线也存在一定的局限性:
1. 曲线复杂度:随着阶数的增加,曲线的复杂度也会增加,计算和绘制过程变得复杂。
2. 误差累积:在多次计算和绘制过程中,贝塞尔曲线的误差会逐渐累积,导致曲线失真。
贝塞尔曲线作为一种优美的数学曲线,在计算机图形学、工业设计、动画制作等领域发挥着重要作用。它不仅丰富了人类对曲线的认识,还为现代科技发展提供了有力支持。在实际应用中,我们还需关注贝塞尔曲线的局限性,以实现更好的设计效果。相信在未来的发展中,贝塞尔曲线将继续为人类创造更多美好事物。






