随着科学技术的不断发展,有限元方法(Finite Element Method,简称FEM)已成为解决复杂工程问题的有力工具。有限元程序作为有限元方法的具体实现,广泛应用于航空航天、建筑、汽车等领域。本文将深入探讨有限元程序的原理、特点及其在工程中的应用,以揭示其神秘面纱。
一、有限元程序的原理

1. 基本概念
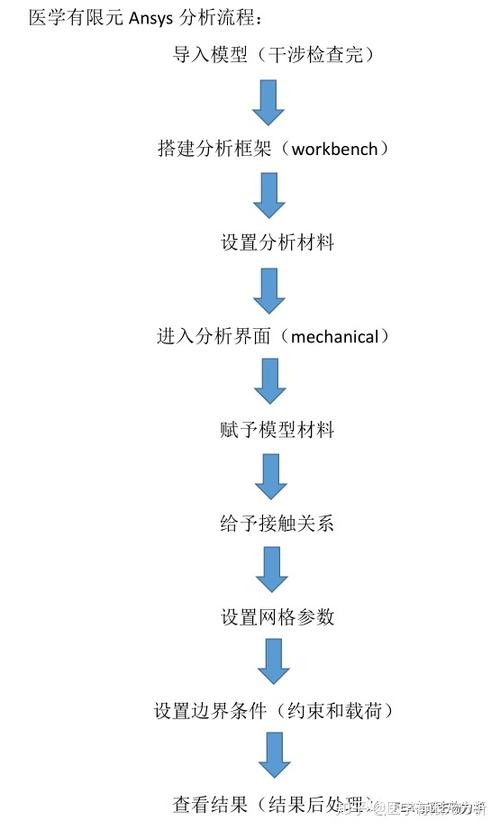
有限元方法是一种数值解法,将连续体离散为有限个单元,通过求解单元内场变量来描述整个结构的场变量分布。有限元程序则是在计算机上实现有限元方法的过程。
2. 离散化
离散化是将连续体离散为有限个单元的过程。有限元程序通常采用以下几种离散化方法:
(1)单元划分:将连续体划分为有限个单元,单元可以是三角形、四边形、六面体等。
(2)节点选取:在每个单元上选取节点,节点是单元内部场变量的离散化代表。
(3)单元属性:定义每个单元的材料属性、几何属性等。
3. 形函数与插值函数
形函数用于描述单元内场变量的分布,插值函数用于计算节点处的场变量。有限元程序中常用的形函数与插值函数有:
(1)线性形函数:适用于线性单元。
(2)二次形函数:适用于二次单元。
(3)三次形函数:适用于三次单元。
4. 单元刚度矩阵
单元刚度矩阵描述了单元内部应力与应变之间的关系。有限元程序通过求解单元刚度矩阵,计算单元内部的应力分布。
5. 总刚度矩阵与载荷矢量
将所有单元刚度矩阵组装成总刚度矩阵,将所有节点载荷组装成载荷矢量。有限元程序通过求解线性方程组,得到整个结构的位移场。
二、有限元程序的特点
1. 广泛的应用范围
有限元程序可以解决各种复杂结构的分析问题,如结构强度、稳定性、动力学、热传导等。
2. 高精度与可靠性
有限元程序具有较高的精度和可靠性,可以满足工程应用的需要。
3. 高效性
有限元程序采用高效的数值计算方法,可以快速求解复杂问题。
4. 通用性
有限元程序具有较好的通用性,可以方便地进行参数化设计、优化设计等。
三、有限元程序的应用
1. 航空航天领域
有限元程序在航空航天领域具有广泛的应用,如飞机结构设计、飞行器结构优化、复合材料结构分析等。
2. 建筑领域
有限元程序在建筑领域具有重要作用,如高层建筑结构分析、桥梁结构设计、地基基础分析等。
3. 汽车领域
有限元程序在汽车领域得到广泛应用,如车身结构设计、碰撞分析、NVH(噪声、振动与粗糙度)分析等。
有限元程序作为一种强大的数值分析工具,在工程领域发挥着越来越重要的作用。随着计算机技术的不断发展,有限元程序将更加完善,为解决复杂工程问题提供有力支持。
参考文献:
[1] 张家勇,有限元方法及其应用[M],北京:清华大学出版社,2010.
[2] 蔡光宪,有限元分析基础[M],北京:机械工业出版社,2012.
[3] 陈惠芳,有限元方法及其应用[M],北京:高等教育出版社,2008.






