自古以来,数学被誉为“科学的皇后”,而函数则是数学世界中的灵魂。在函数家族中,有一种特殊的函数——幂函数,它以其独特的魅力,吸引了无数数学爱好者的目光。本文将带领大家走进幂函数的世界,领略其无穷的魅力。
一、幂函数的定义与性质

1. 定义
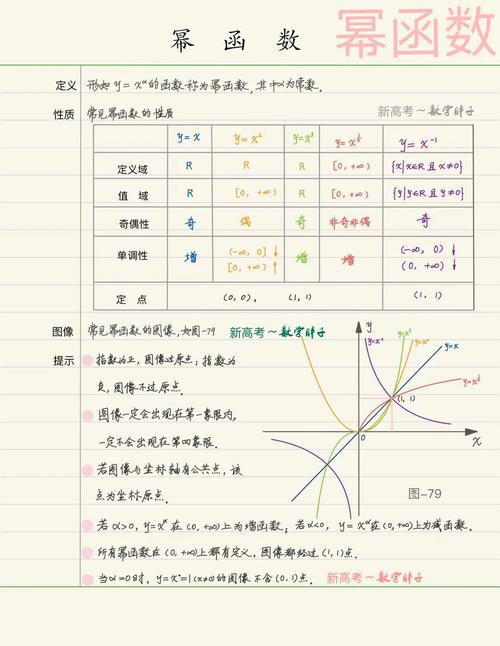
幂函数是一种以指数形式表示的函数,其一般形式为f(x) = x^a,其中x是自变量,a是指数。当指数a为正整数时,称为幂函数;当指数a为负整数时,称为倒幂函数;当指数a为分数时,称为有理幂函数。
2. 性质
(1)幂函数在实数范围内有定义,且定义域为全体实数。
(2)幂函数的图像是一个抛物线,开口方向取决于指数a的正负。
(3)当a为正整数时,幂函数在x=0处连续,且在x=0处可导;当a为负整数时,幂函数在x=0处间断,且在x=0处不可导。
(4)幂函数在定义域内单调性明显,当a>0时,函数在定义域内单调递增;当a<0时,函数在定义域内单调递减。
二、幂函数的应用
1. 自然科学
在自然科学领域,幂函数广泛应用于描述物体运动、能量转换等物理现象。例如,牛顿第二定律F=ma中,物体的加速度a与力F成正比,而力F与物体的质量m成正比,因此加速度a与质量m的乘积Fm成正比,即a∝Fm,可表示为a = kF^m,其中k为常数,m为指数。
2. 经济学
在经济学领域,幂函数常用于描述经济现象,如需求、供给、生产等。例如,拉格朗日需求函数Q(p) = A/p^b,其中Q为需求量,p为价格,A和b为常数,该函数表示需求量与价格的关系。
3. 生物学
在生物学领域,幂函数可用于描述种群增长、物种分布等生物现象。例如,孟德尔遗传定律中,显性基因与隐性基因的比例关系可以用幂函数表示。
三、幂函数的数学意义
1. 数学之美
幂函数以其简洁、优美、富有表现力的形式,展现出数学之美。它揭示了事物之间普遍存在的规律,使人们更好地认识世界。
2. 数学发展
幂函数的发展推动了数学的进步。从初等数学到高等数学,幂函数的应用越来越广泛,为数学理论体系的构建提供了有力支持。
幂函数作为一种特殊的函数,具有丰富的内涵和广泛的应用。在数学、自然科学、经济学、生物学等领域,幂函数都发挥着重要作用。让我们一起走进幂函数的世界,感受数学之美,探索无穷的奥秘。





