在数字电路的世界里,半加器是一个不可或缺的基石,它承载着数字电路设计的智慧之光。半加器,顾名思义,是指只完成两个一位二进制数相加,而不考虑进位的加法器。这个看似简单的电路,却蕴含着丰富的数学原理和逻辑思维。
一、半加器的构成与工作原理

半加器的构成相对简单,主要由两个输入端和一个输出端组成。输入端分别为两个一位二进制数A和B,输出端为一个一位二进制数S,表示A和B的和。还有一个进位输出端C,用于表示A和B相加时是否产生进位。
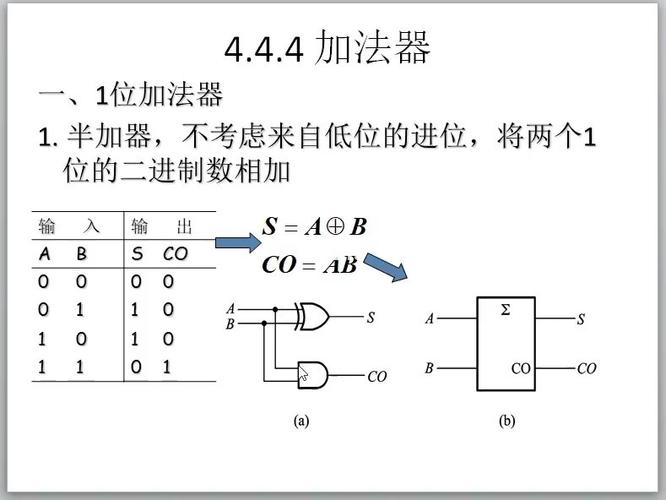
半加器的工作原理如下:当两个一位二进制数A和B相加时,若它们的和小于等于1,则无进位,输出端S直接输出A和B的和;若它们的和大于等于2,则产生进位,输出端S输出1,进位输出端C输出1。
二、半加器的应用与扩展
半加器在数字电路中有着广泛的应用,如:
1. 数字电路中的基本运算:半加器是实现二进制加法运算的基础,通过级联多个半加器,可以构成多位二进制加法器。
2. 算术逻辑单元(ALU):半加器是构成ALU的基本模块之一,用于实现各种算术运算和逻辑运算。
3. 寄存器:半加器可用于构建寄存器,实现数据的暂存和传输。
4. 指令译码器:半加器可用于指令译码器,实现指令的识别和执行。
除了上述应用,半加器还可以进行以下扩展:
1. 全加器:全加器是半加器的扩展,它考虑了进位的影响,可以实现多位二进制数的加法运算。
2. 多功能加法器:通过级联多个半加器,可以构成多功能加法器,实现多种运算功能。
三、半加器的数学原理与逻辑思维
半加器的设计与实现,涉及到数学原理和逻辑思维。以下是半加器设计中的几个关键点:
1. 异或(XOR)运算:半加器的输出端S是由两个输入端A和B进行异或运算得到的。异或运算的原理是:当两个输入端不输出端为1;当两个输入端相输出端为0。
2. 与(AND)运算:半加器的进位输出端C是由两个输入端A和B进行与运算得到的。与运算的原理是:当两个输入端都为1时,输出端为1;否则输出端为0。
3. 逻辑思维:半加器的实现过程,需要运用逻辑思维,分析各个输入端和输出端之间的关系,从而设计出符合要求的电路。
半加器作为数字电路中的基石,承载着数字电路设计的智慧之光。通过对半加器的深入研究,我们可以更好地理解数字电路的原理和设计方法,为我国数字电路领域的发展贡献力量。
参考文献:
[1] 张立新,数字电路与逻辑设计[M],清华大学出版社,2010年。
[2] 王宇,数字逻辑与数字电路[M],机械工业出版社,2008年。
[3] 刘瑞,数字电路与逻辑设计[M],高等教育出版社,2015年。






