自古以来,数学便以其严谨的逻辑和深邃的内涵,吸引着无数人的目光。在数学的众多分支中,质因数分解以其独特的魅力,成为了人们研究数学问题的重要工具。本文将探讨质因数分解的原理、应用及其在编程领域的应用,以揭示数学之美与编程之魅。
一、质因数分解的原理

质因数分解是将一个正整数分解为若干个质数的乘积的过程。质数是指只能被1和自身整除的数,如2、3、5、7等。一个合数可以分解为若干个质数的乘积,这些质数称为合数的质因数。
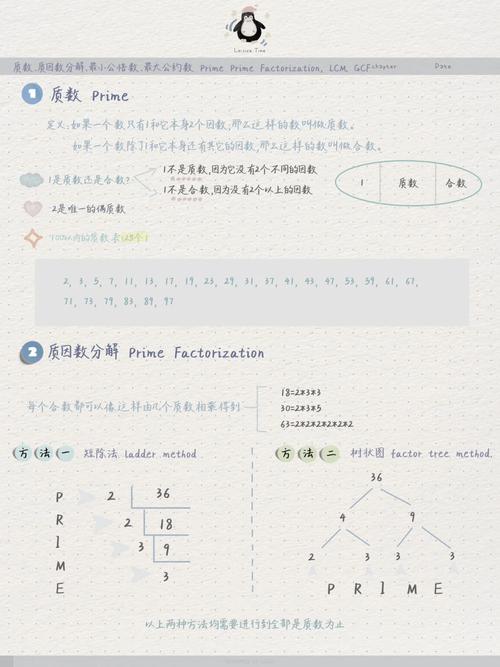
例如,将60分解为质因数的过程如下:
60 = 2 × 30
= 2 × 2 × 15
= 2 × 2 × 3 × 5
由此可见,60的质因数有2、3、5,且2和3都是质数,5也是质数。
二、质因数分解的应用
质因数分解在数学领域有着广泛的应用,以下列举几个例子:
1. 数论:质因数分解是数论研究的基础,许多数论问题都与质因数分解密切相关。
2. 编码理论:在密码学中,质因数分解被应用于公钥加密算法,如RSA算法。
3. 计算几何:在计算机图形学中,质因数分解可以用于优化算法,提高计算效率。
4. 概率论:在概率论中,质因数分解可以用于求解随机变量分布问题。
三、质因数分解在编程领域的应用
随着计算机技术的不断发展,质因数分解在编程领域得到了广泛应用。以下列举几个例子:
1. 加密算法:公钥加密算法如RSA算法,其安全性依赖于大整数的质因数分解难度。编程人员通过实现质因数分解算法,为加密算法提供安全保障。
2. 大整数运算:在编程中,经常需要对大整数进行运算。为了提高运算效率,编程人员可以利用质因数分解将大整数分解为质数乘积,从而简化运算过程。
3. 算法优化:在计算机科学中,算法优化是提高程序性能的关键。通过质因数分解,编程人员可以优化算法,降低时间复杂度和空间复杂度。
4. 数据分析:在数据分析领域,质因数分解可以用于分析数据分布,提取有价值的信息。
质因数分解作为数学与编程的交汇点,既展示了数学之美,又彰显了编程之魅。通过对质因数分解原理和应用的研究,我们可以更好地理解数学与编程之间的联系,从而提高编程技能和解决实际问题的能力。在未来,质因数分解将在更多领域发挥重要作用,为我国科技创新贡献力量。
质因数分解作为一种重要的数学工具,在编程领域具有广泛的应用前景。掌握质因数分解原理及其应用,有助于我们更好地理解数学之美和编程之魅,为我国科技事业的发展助力。














