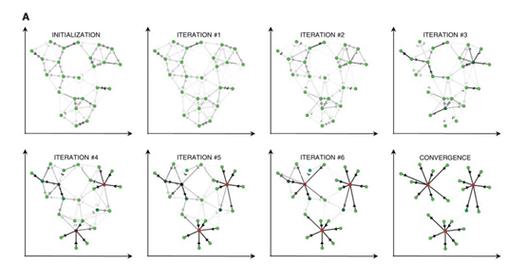
Affinity Propogation算法的事理可以大略的概括为:每一个数据点都会给其它的多有点发送信息,奉告其它所有点每个目标对发送者(sender)的相对吸引力的目标值(target)。
随后,鉴于从所有其它sender收到信息的“attractiveness”,每个target所有sender一个回答,以奉告与sender相联系的每一个sender的可用性。sender会给target回答干系信息,以奉告每一个target对sender改动的相对“attractiveness”(基于从所有target收到的关于可用性的信息)。信息通报的全体过程直到达成同等才会停滞。

一旦sender与某个target相联系,这个target就会称为该点(sender)的“范例代表(exemplar)”。所有被相同exemplar标记的点都被放置在一个聚类中。
假定一个如下的数据集。每一个参与者代表一个五维空间的数据点。
相似性矩阵(C)
除了在对角线上的元素外,其它的元素是负的均方偏差作为两个数据间的相似值。
打算公式如下:c(i, j) = -||X_i-X_y||^2c(i,j)=−∣∣Xi−Xy∣∣2以Alice和Bob为例,两者间的相似性打算过程如下:(3-4)^2+(4-3)^2+(3-5)^2+(2-1)^2+(1-1)^2 = 7(3−4)2+(4−3)2+(3−5)2+(2−1)2+(1−1)2=7。
因此,Alice与Bob之间的相似值为-7。
相似性值的打算边界涌如今Bob和Edna间:(4-1)^2+(3-1)^2+(5-3)^2+(1-2)^2+(1-3)^2 = 22(4−1)2+(3−1)2+(5−3)2+(1−2)2+(1−3)2=22Bob和Edna之间的相似值为-22。
通过逐步的打算,末了得到的结果如下:
一样平常对角线上的元素取相似值中较小的数,在本例中取值为-22,因此,得到的相似性矩阵如下:
Responsibility Matrix ®
这里的responsibility matrix 是中间的过度步骤。通过利用如下的公式打算responsibility matrix:r(i, k ) \leftarrow s(i, k)- max_{k^{'} such\ that\ k^{'} \not= \ k} \{a(i, k^{'})+s(i, k^{'})\},r(i,k)←s(i,k)−maxk′such that k′= k{a(i,k′)+s(i,k′)},个中,i表示协同矩阵的行,k表示列的关联矩阵。
例如,r(Alice, Bob)r(Alice,Bob)的值为-1, 首先提取similarity matrix中c(Alice, Bob)c(Alice,Bob)的值为-7, 减去similarity matrix中Alice行的最大值为-6,因此,得到r(Alice, Bob)=-1r(Alice,Bob)=−1。
取值的边界为r(Cary, Doug)r(Cary,Doug),其打算如下:
r(Cary, Doug) = -18-(-6)=-12r(Cary,Doug)=−18−(−6)=−12
根据上述公式打算得到的终极结果如下图所示:
Availability Matrix (a)
Availability Matrix的初始值为矩阵中的所有元素均为0。
首先,打算对角线上的元素值:a(k,k) \leftarrow \sum_{i^{'}such \ that \ i^{'} \not= k} max\{0, r\{i^{'}, k\}\},a(k,k)←i′such that i′=k∑max{0,r{i′,k}},个中,i表示协同矩阵的行,k表示协同矩阵的列。
实际上,上面的公式只见告你沿着列,打算所有行与0比较的最大值(除列序与行序相等时的情形除外)。
例如,a(Alice, Alice)a(Alice,Alice)的打算如下:a(Alice, Alice) = 10+11+0+0 = 21a(Alice,Alice)=10+11+0+0=21
其次,打算非对角线上的元素值,分别以a(Alice, Cary)a(Alice,Cary)和a(Doug, Edna)a(Doug,Edna)为例,其打算过程如下所示:
a(Alice, Cary) = 1+0+0+0 = 1 \\ a(Doug, Edna)
= 0+0+0+9 = 9a(Alice,Cary)
=1+0+0+0=1a(Doug,Edna)
=0+0+0+9=9
以下公式是用于更新Availability Matrix,其公式如下:a(i, k) \leftarrow min\{0, r(k,k)+\sum_{i^{'} such \ that \ i^{'} \notin \{i, k\}} max{\{0, r(i^{'}, k)}\}\}a(i,k)←min{0,r(k,k)+i′such that i′∈/{i,k}∑max{0,r(i′,k)}}
当你想要更新a(Alice, Bob)a(Alice,Bob)的值时,其打算过程如下:a(Doug, Bob) = min\{{0,(-15)+0+0+0}\}=-15a(Doug,Bob)=min{0,(−15)+0+0+0}=−15末了得到的结果如下表所示:
Criterion Matrix ©
在得到上面的availability matrix后,将availability matrix和responsibility matrix的对应元素相加,便可得到criterion matrix。
其打算公式如下:c(i, k) \leftarrow r(i,k)+a(i,k).c(i,k)←r(i,k)+a(i,k).末了得到的criterion matrix的结果如下:
以上便是Affinity Propogation算法的打算过程,这是我见过最浅近易懂的讲解了,详见原文。
代码示例如下:
首先,导入干系库:
import numpy as npfrom matplotlib import pyplot as pltimport seaborn as snssns.set()from sklearn.datasets.samples_generator import make_blobsfrom sklearn.cluster import AffinityPropagation
利用scikit-learn天生须要的数据集,详见如下:
X, clusters = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)plt.scatter(X[:,0], X[:,1], alpha=0.7, edgecolors='b')
演习模型(由于是无监督算法,因此不须要拆分演习集和测试集):
af = AffinityPropagation(preference=-50)clustering = af.fit(X)
末了,将不同聚类的点可视化:
plt.scatter(X[:,0], X[:,1], c=clustering.labels_, cmap='rainbow', alpha=0.7, edgecolors='b')
算法利用场景:
Affinity Propagation是一个无监督的机器学习算法,它尤实在用于那些不知道最佳聚类数情形的算法。
(1)获取更多优质内容及精彩资讯,可前往:https://www.cda.cn/?seo
(2)理解更多数据领域的优质课程:






